论文地址：[2312.10588] Post-Training Quantization for Re-parameterization via Coarse & Fine Weight Splitting

摘要

尽管神经网络在各类应用中取得了显著进展，但它们需要大量的计算和内存资源。网络量化是一种强大的神经网络压缩技术，能够实现更高效、可扩展的人工智能部署。最近，重参数化作为一种有前景的技术崭露头角，它可以在提升模型性能的同时减轻各类计算机视觉任务中的计算负担。然而，在重参数化网络上应用量化时，准确率会显著下降。我们发现，主要挑战源于原始分支间权重分布的巨大差异。为解决这一问题，我们提出一种粗 - 细权重拆分（CFWS）方法以降低权重的量化误差，并开发一种改进的KL度量来确定激活的最优量化尺度。据我们所知，我们的方法是首项使得后训练量化可应用于重参数化网络的工作。例如，量化后的RepVGG - A1模型准确率仅损失0.3%。代码位于https://github.com/NeonHo/Coarse-Fine-Weight-Split.git

1. 引言

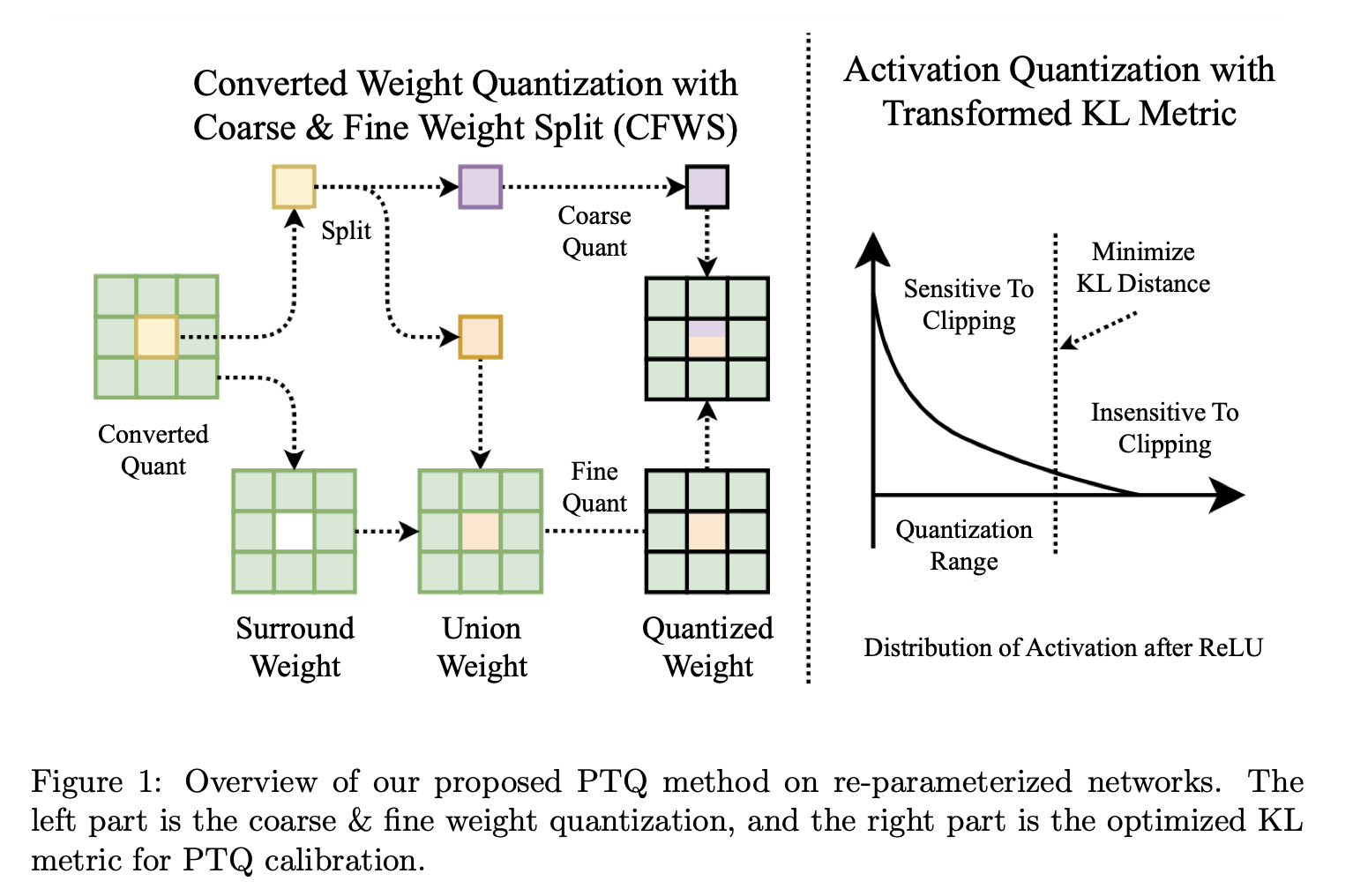
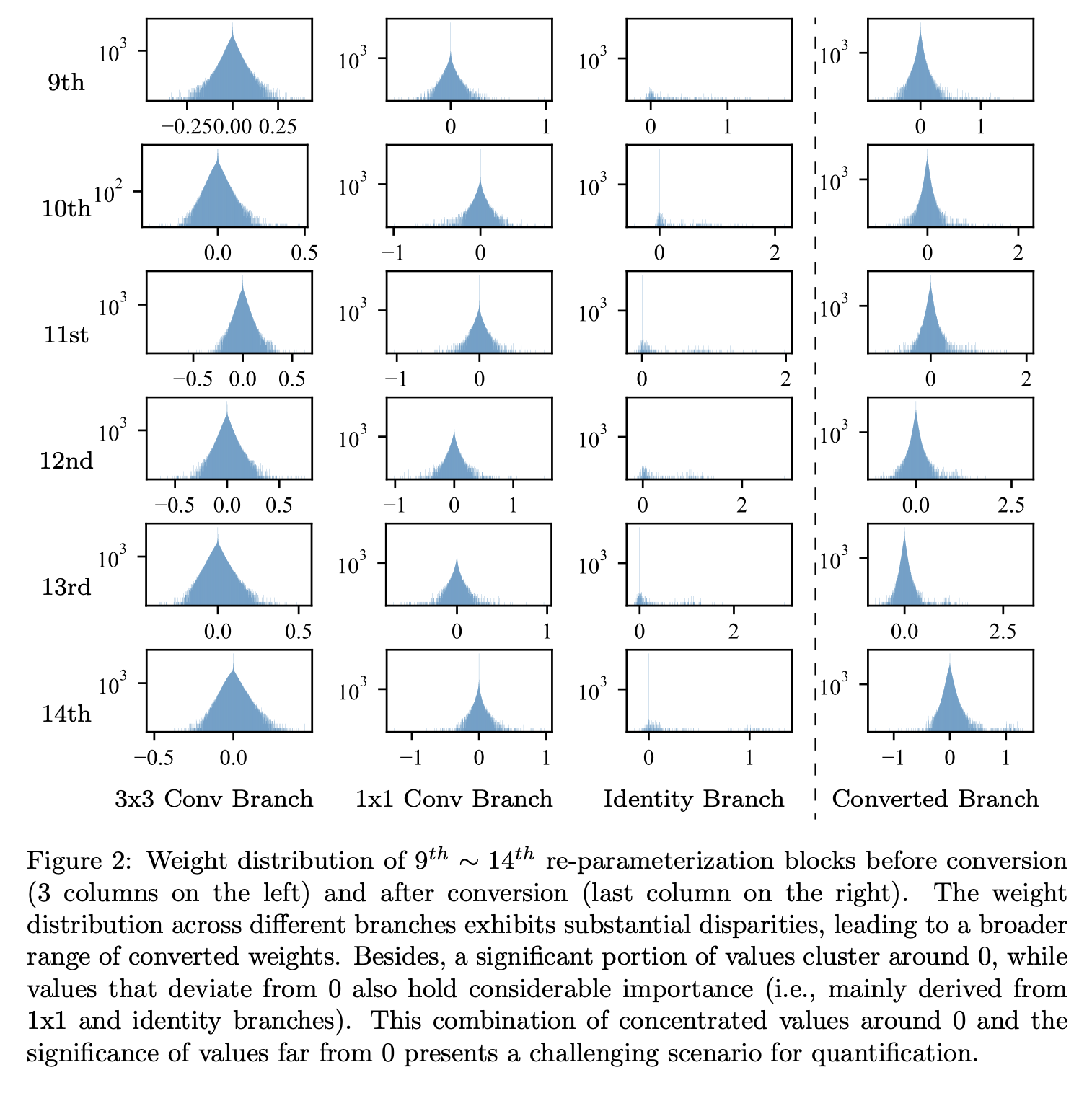
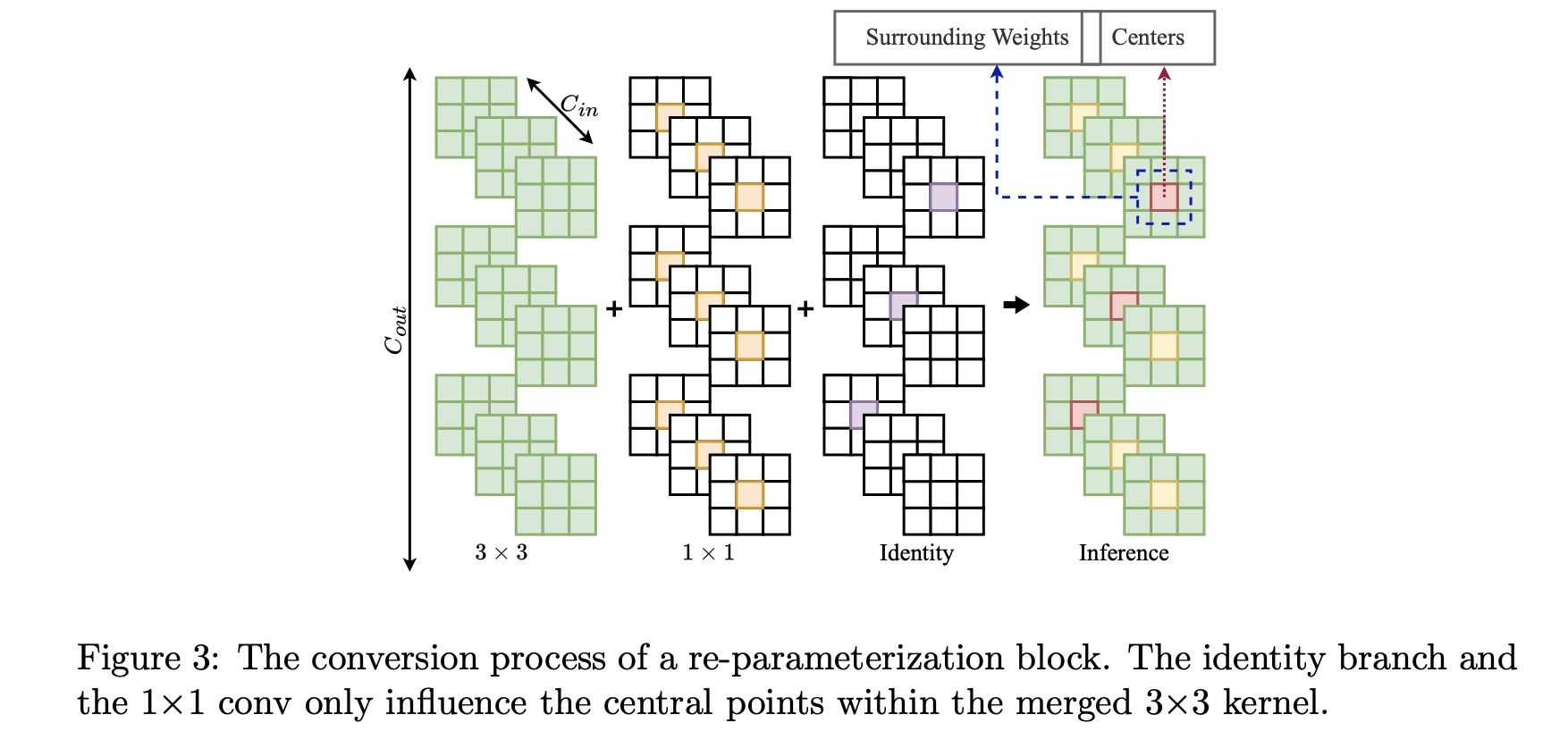
虽然卷积神经网络（CNNs）在广泛的应用领域展现出卓越性能，但人们仍期望其在边缘设备和云服务器上都能高效运行。神经网络量化[1, 2, 3, 4, 5, 6]是最常用的神经网络压缩技术之一。它涉及降低网络参数和激活值的精度，通常是从浮点数（如FP32）转换为低比特整数（如INT8）。这大幅降低了内存成本（例如，INT8节省75%的模型大小和带宽），并且由于整数运算加速了矩阵乘法（如卷积、全连接层）。网络量化通常分为两类：训练后量化（PTQ）[2, 6]和量化感知训练（QAT）[4, 5]。PTQ对已训练好的网络进行量化，只需少量数据或无需数据，因此几乎无需调整超参数，也无需端到端训练。相比之下，QAT是在模型训练或重新训练过程中进行模拟量化。所以它通常需要大量计算资源，并且在训练（如超参数调整）上要付出更多努力，导致部署过程复杂。此外，在部署神经网络时，由于隐私或数据安全问题[2]，获取训练资源（如训练数据、训练代码）可能会受到限制。因此，在本文中，我们特别关注将PTQ应用于重参数化网络。 最近，重参数化[7]作为一种有前景的技术出现，并在各种任务中得到广泛应用[8, 9, 10, 11, 12]。它是用一组线性层替换每个线性层，如全连接层（FC）和卷积层（Conv）。这种模块仅在训练期间使用，在推理时最终会合并为单个线性层。一方面，重参数化在训练期间利用其多分支架构的出色性能。另一方面，转换后的简单单分支结构利用其高并行性和较小的内存占用，从而提高推理效率。例如，开创性工作RepVGG [7]在ImageNet上达到超过80%的Top - 1准确率，并且比ResNet - 50 [13]运行速度快83%，准确率更高。众所周知，ResNet的残差路径需要实时保留内存，这对于资源受限的边缘设备来说可能具有挑战性。然而，直接在重参数化网络上应用量化方法时，准确率会显著下降。例如，RepVGG - A1在PTQ后准确率从74.5%降至61.7%。量化后的重参数化模型准确率下降，阻碍了它们的实际应用。 值得一提的是，由于重参数化网络在部署模式下没有批量归一化（BN）层，通过QAT提高量化精度也很困难。 据我们目前所知，只有两篇论文[14, 15]探索了重参数化网络的量化。然而，尽管它们具有创新性，但这两种方法都需要对原始重参数化结构进行修改。具体来说，[15]将BN层移到重参数化模块（rep - block）之外；[14]放弃了重参数化结构，而是在优化器中加入重参数化。虽然转换后的单分支在推理时结构保持不变，但训练过程变得明显更加复杂，在训练流程中需要额外的时间、步骤和调整。此外，这两种方法都需要从头开始训练修改后的模型，这是一个重大限制。相比之下，我们的目标是确保模型研究和模型部署保持独立：（1）让研究人员专注于改进浮点模型的结构和准确率，而不受量化过程的阻碍。（2）简化部署过程。第二点至关重要，因为从头开始训练模型并不总是可行的，特别是在缺乏可用数据集的场景中（例如，模型由供应商提供或数据集保密时），或者需要快速部署，又或者在训练成本方面存在限制时。 为了在重参数化网络上应用PTQ而不导致显著的准确率下降，我们对这项任务进行了研究，以确定主要挑战。我们发现量化困难是由于原始分支间权重分布的巨大差异造成的，这导致融合内核的参数分布不理想。如图2所示，不同分支的权重分布存在显著差异，导致转换后的权重范围更宽。例如，在第12个卷积分支中，3x3卷积、1x1卷积和恒等分支的范围分别约为[-0.8, 0.8]、[-1.2, 1.8]和[-0.2, 2.8]；转换后最终范围扩展到[-1.2, 2.8]。观察可知，很大一部分值集中在0附近，而偏离0的值也相当重要（即主要来自1x1和恒等分支）。这种值集中在0附近且远离0的值也很重要的情况，给量化带来了挑战。 我们根据转换过程进一步研究这个问题（如图3所示），恒等分支和1×1卷积的权重仅影响合并后的3×3内核中的中心点。具体来说，转换后内核的中心点值范围很宽，而周围的权重（即3×3矩阵中的八个非中心点）范围较小（更多细节见图4）。[14]也指出，内核的中心点相比周围点具有更高的标准差。因此，我们的重点应该是对转换后内核中的中心点进行适当量化。 我们提出粗 - 细权重拆分（CFWS）方法，分别对中心权重和周围权重进行量化。在激活量化方面，我们注意到许多较大的激活值对裁剪不敏感。这一观察促使我们提出一种基于KL散度[16]的校准度量。改进后的度量能够对较大的激活值进行适当裁剪，从而有效减轻量化误差。 我们在为不同任务设计的各种重参数化网络上评估了所提出的PTQ方法。结果表明，我们的方法不仅对图像分类有效，而且在目标检测任务中也展现出良好的泛化能力。我们的贡献如下：

1) 我们为重参数化网络提出了一种新颖的PTQ方法，无需对网络进行任何修改或重新训练。我们的方法有效地弥合了重参数化技术与PTQ实际部署之间的差距。 2) 我们分析了基于重参数化架构的量化中性能下降的根本原因，并提出了一种名为粗 - 细权重拆分（CFWS）的新技术。这种方法能够分别对中心权重和周围权重进行量化，有效解决了该问题。 3) 我们开发了一种改进的KL度量，能够平稳地处理对较大激活值的适当裁剪。我们的整体方法在各种视觉任务上具有良好的泛化性，并实现了具有竞争力的量化准确率，同时保留了PTQ快速部署的优势。

2. 背景与相关工作

2.1 量化

神经网络量化是深度学习中用于降低神经网络内存和计算需求的一种技术[1, 2, 3, 4, 5, 6]。与标准浮点表示相比，它使用更少的比特数来表示神经网络的权重和激活值。通常，深度神经网络将权重和激活值存储为32位浮点数，但使用低精度表示可以显著减少内存使用并提高计算效率。例如，用8位整数（INT8）代替32位浮点数（FP32），可使模型大小和带宽减少75%，并且由于整数运算，还能加速矩阵乘法（如卷积、全连接层）。 网络量化主要可分为两种方法：训练后量化（PTQ）[2, 6]和量化感知训练（QAT）[4, 5]。PTQ是对预训练好的网络进行量化，只需极少数据或无需数据，几乎无需调整超参数，也无需端到端训练。另一方面，QAT是在模型训练或重新训练过程中通过模拟量化来实现。QAT通常需要大量计算资源以及更多的训练投入，比如超参数调整，这导致部署过程较为复杂。此外，由于隐私或数据安全问题，部署神经网络时获取训练数据可能会受到限制[2]。由于QAT涉及修改训练代码并需要额外成本，因此仅在训练资源（代码和数据）可用且PTQ无法产生满意结果时才会使用。在本文中，我们特别关注将PTQ应用于重参数化网络。

2.2 重参数化

重参数化并非新概念，其可追溯到批归一化[17]和残差连接[13]。丁等人[7]最近提出了RepVGG网络架构，该架构采用了结构重参数化。从那时起，重参数化展现出良好前景，并在各种任务中得到广泛应用[8, 9, 10, 11, 12, 18]。基本上，它是用一组线性层替换每个线性层，如全连接层（FC）和卷积层（Conv）。这种模块仅在训练期间使用，在推理时最终会合并为单个线性层。转换后的网络在推理时能达到与训练时相同的预测精度。 重参数化具有几个优点。首先，它利用了多分支架构的卓越性能和更快的收敛速度。其次，转换后的简单单分支结构利用了高并行性和较小的内存占用，从而提高了推理效率。例如，开创性工作RepVGG [7]在ImageNet上的Top - 1准确率超过80%，比ResNet - 50 [13]运行速度快83%，比ResNet - 101快101%，且准确率更高。众所周知，ResNet的残差路径需要实时保留内存，这对于资源受限的边缘设备来说颇具挑战。尽管重参数化在准确率和速度方面都具有明显优势，但量化后的重参数化模型准确率下降，阻碍了它们的实际应用[15]。

2.3 重参数化网络量化的探索

基于重参数化的架构由于其固有的多分支设计，在量化方面带来了挑战，这会导致动态数值范围增大。目前，仅有两篇研究[14, 15]探索过重参数化网络的量化。丁等人[14]引入了梯度重参数化（GR）方案，通过将先验知识融入一种名为RepOptimizer的特定网络优化器来取代重参数化。朱等人[15]将RepVGG重新设计为QARepVGG，生成了针对量化优化的权重和激活分布。然而，这两种方法都需要对原始重参数化结构进行修改。具体而言，[15]将批归一化（BN）层移到重参数化模块（rep - block）之外，而[14]则去掉了重参数化结构并将其整合到优化器中。尽管转换后的单分支在推理时结构保持不变，但训练过程变得明显更加复杂，在训练流程中需要额外的时间、步骤和调整。相比之下，我们的方法保持了模型研究与PTQ部署的独立性。

3. 方法

量化函数旨在将浮点向量(X)转换为定点值(X_q)。对称均匀量化(Q)是最常见的方法[1]，其公式为：

量化误差(X - X_q)通常有两个来源：舍入函数产生的误差称为舍入误差，而clip函数产生的误差称为裁剪误差。量化范围之外的值称为离群值，将被裁剪。 在神经网络上应用量化时，与浮点网络性能的接近程度是评估量化方法有效性的主要标准。一般的量化目标为：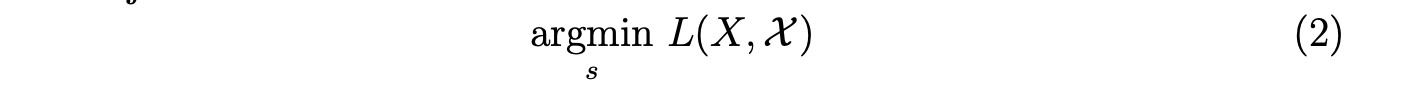

其中(L)是一个目标函数，如均方误差（MSE）。我们的目标是找到合适的(s)和(L)值，以在不产生额外重新训练成本的情况下最大化量化网络的性能。 在以下小节中，我们首先分析基于重参数化架构的量化中性能下降的潜在原因，然后介绍我们针对重参数化网络中权重和激活量化的训练后量化（PTQ）方法。

3.1 粗 - 细权重拆分

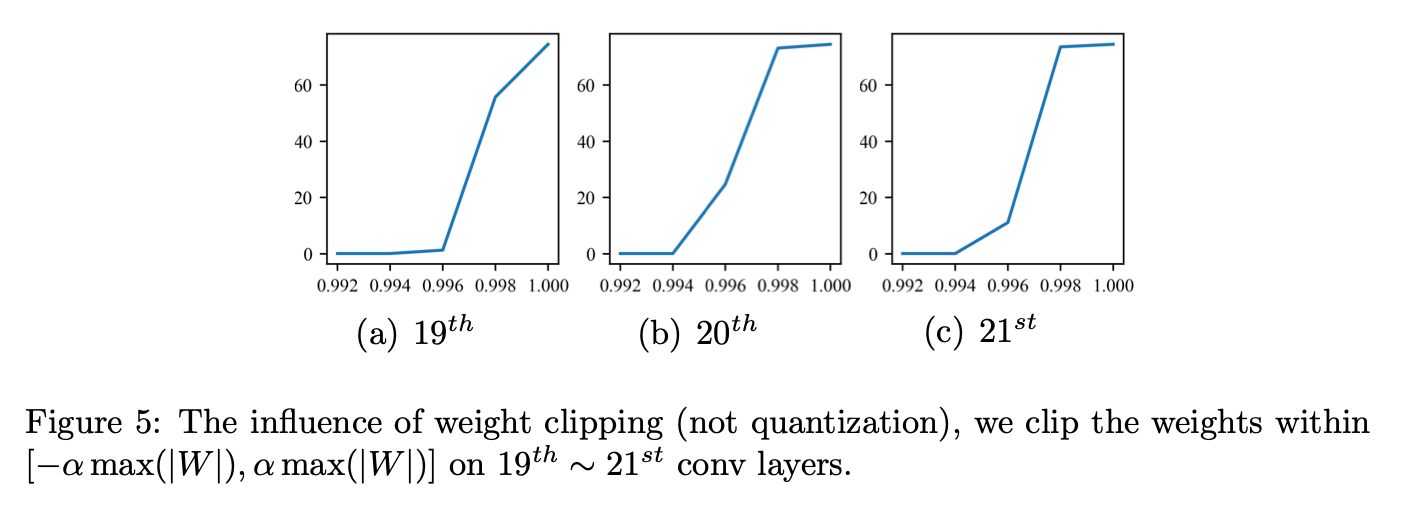
为便于理解，我们在图2中可视化了RepVGG模块转换前后的权重分布。不同分支的权重分布存在显著差异，导致转换后的权重范围更宽。例如，在第12个卷积分支中，3x3卷积、1x1卷积和恒等分支的范围分别约为([-0.8, 0.8])、([-1.2, 1.8])和([-0.2, 2.8])；转换后最终范围扩展到([-1.2, 2.8])。观察可知，很大一部分值集中在0附近，而偏离0的值也相当重要（即主要来自1x1和恒等分支）。这种值集中在0附近且远离0的值也很重要的情况，给量化带来了挑战。[19]指出，遵循均匀分布的权重对量化更具抗性。在我们的情况下，直接应用如MinMax这样的PTQ方法会导致量化范围过宽。这个宽范围可能导致在量化过程中，集中在小区间内的很大一部分权重丢失，从而削弱卷积层保持其原始特征提取能力。 我们根据转换过程进一步研究这个问题（如图3所示），恒等分支和1×1卷积的权重仅影响合并后的3×3内核中的中心点。具体来说，转换后内核的中心点值范围很宽，而周围的权重（即3×3矩阵中的八个非中心点）范围较小（更多细节见图4）。我们发现，转换后的卷积权重分布范围宽主要源于中心点附近的分布。[14]也指出，内核的中心点相比周围点具有更高的标准差。然后我们分析权重对裁剪的敏感性。如图5所示，对转换后的权重进行轻微裁剪将导致预测准确率大幅下降。上述分析促使我们为重心中的权重寻找更好的量化技术。 为解决该问题，我们提出粗 - 细权重拆分（CFWS）方法，分别对中心权重和周围权重进行量化。给定转换后的卷积权重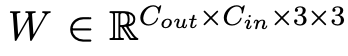，其中(C_{out})和(C_{in})分别表示输出通道数和输入通道数，整个过程可视为：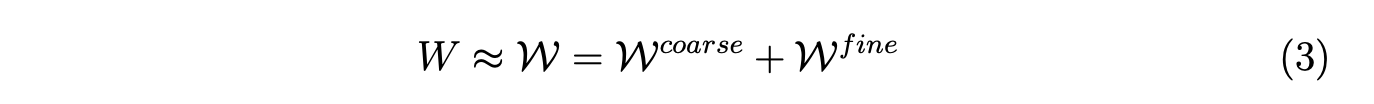

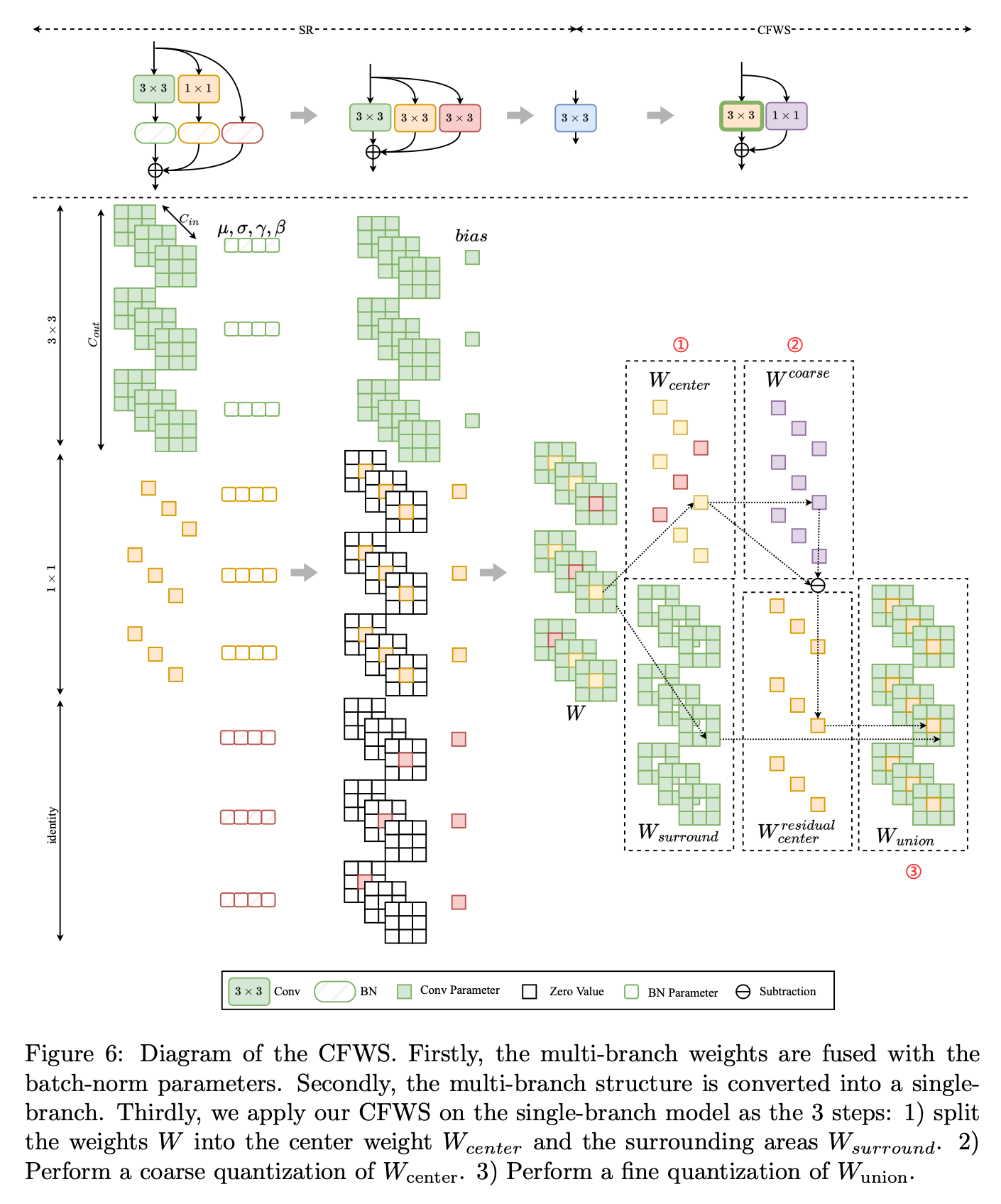
如图6所示，我们的CFWS主要包括3个步骤：

1. 权重拆分：

2. 中心权重粗量化：

   由于此步骤涉及粗量化，因此有必要补偿残差，即：

3. 合并权重细量化：

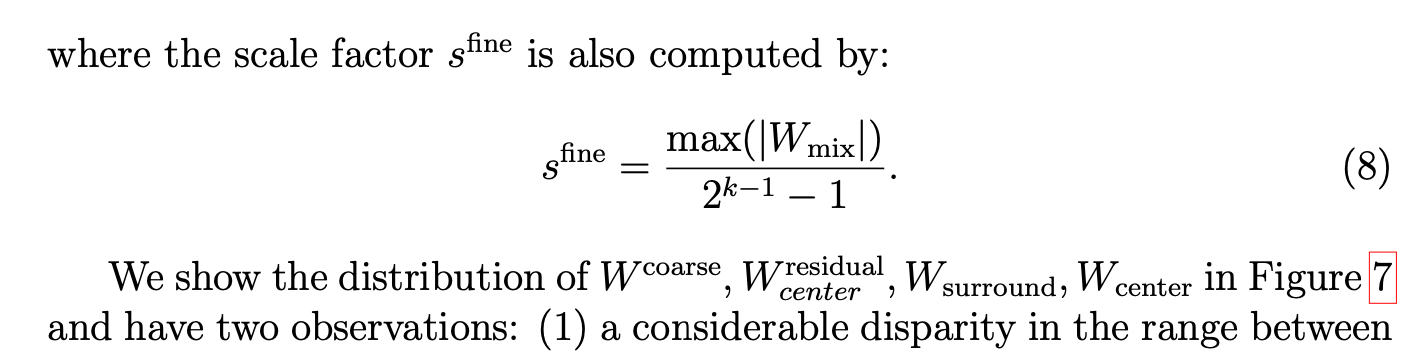
通过观察这几个weight的分布，得到两个观察结果：(1) (W_{surround})和(W_{center})之间的范围存在显著差异；(2) 大多数值集中在零附近的狭窄范围内，只有少数值是离群值。通过采用我们提出的CFWS，(W_{center})和(W_{surround})的量化误差都显著降低。对于(W_{center})，粗量化误差由后续的细量化补偿。对于(W_{surround})，其量化范围被调整以减轻(W_{center})中较大值的影响。

为了在不依赖特定目标平台的情况下评估我们提出的CFWS的效率，我们采用比特运算（BOPs）[21, 22, 23]作为替代指标。BOPs定义如下：

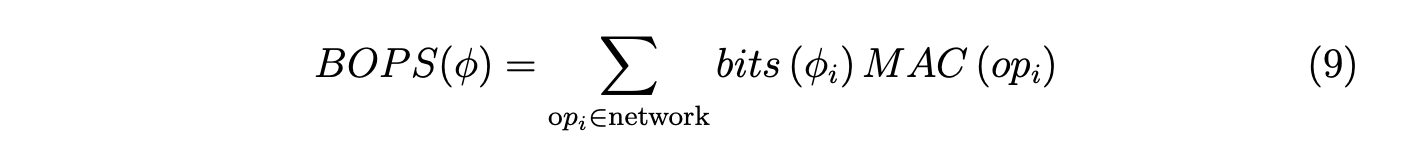
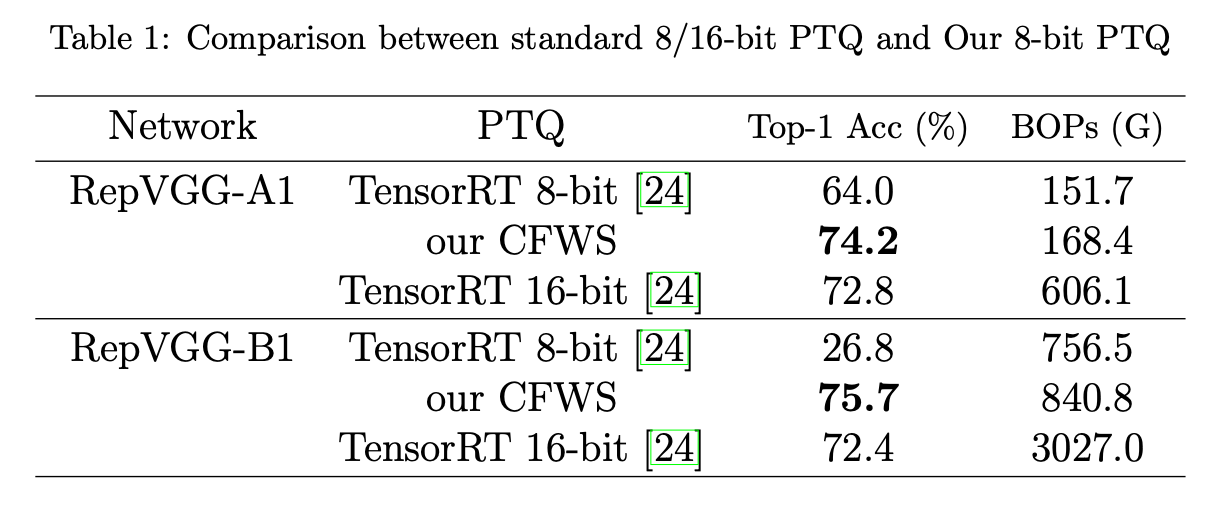
其中(op_i)表示网络中执行的操作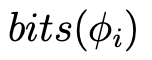，表示与操作(op_i)的权重和激活相关的比特宽度，(MAC(op_i))表示操作(op_i)的乘加（MAC）操作总数。在表1中，值得注意的是，与INT8量化相比，我们的方法在准确率上有显著提升，而比特运算（BOPs）增加极少。此外，与INT16量化相比，我们的方法不仅实现了更高的准确率，而且所需的BOPs显著更少。

#### 3.2 激活量化指标

在分析激活分布时，我们引入一种方法来分析激活裁剪的影响。我们手动设置每个卷积层激活值的裁剪范围，并通过改变裁剪范围观察对ImageNet验证集上网络准确率的影响。这使我们能够了解不同值的激活的重要性。具体实现如下：

1. 向网络输入一些输入样本，并收集每层的激活值(A)。

2. 计算(A)的最大绝对值(\max(

   A

   ))。

3. 将(A)裁剪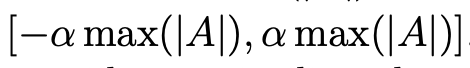到范围内。此范围内的数据保留，外部部分裁剪为

4. 逐步减小(\alpha)以缩小范围。在每一步中，收集网络的预测准确率。

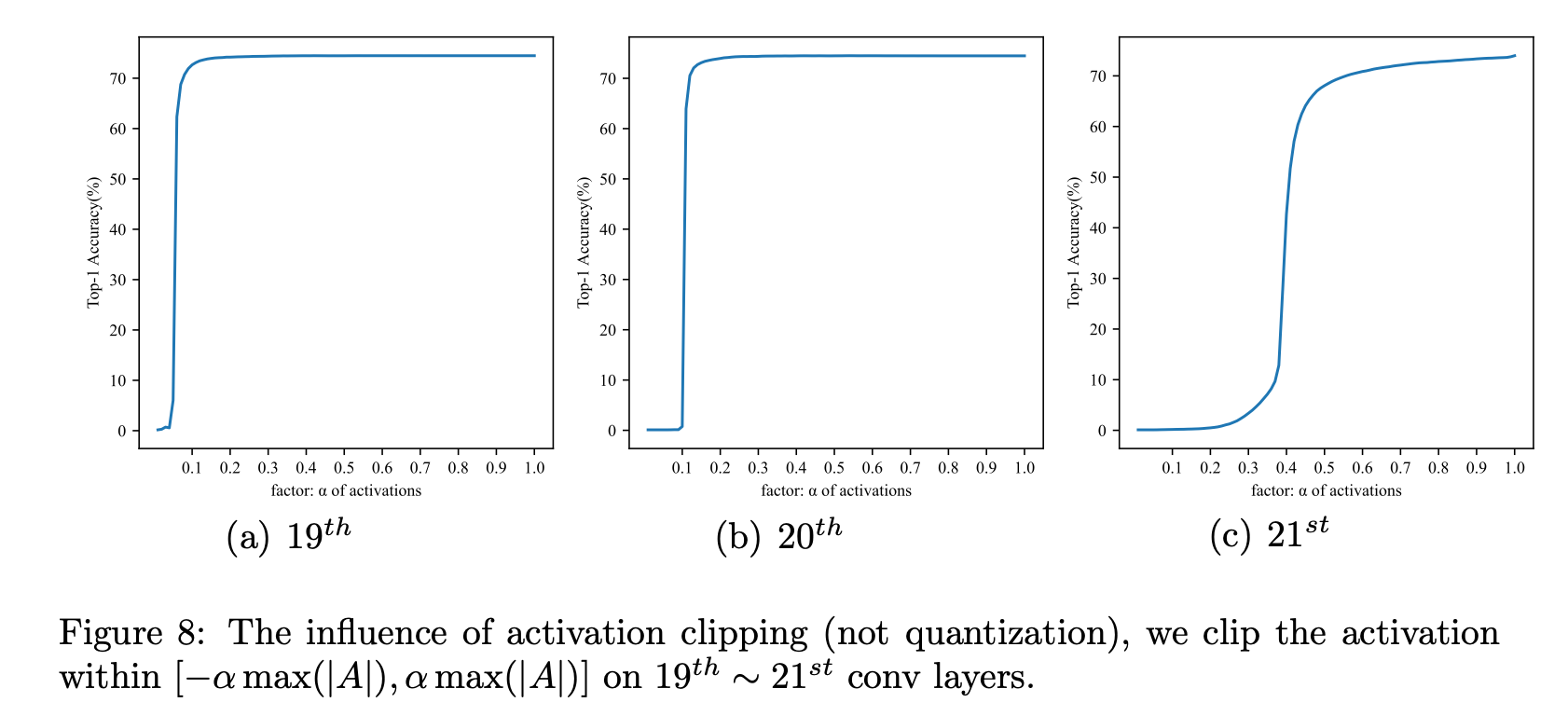
   网络的alpha-accuracy曲线绘制在图8中。我们发现激活值分布中的较大值不会影响网络的整体准确率，经过适当裁剪后准确率甚至可能提高。换句话说，激活中存在大量对裁剪不敏感的离群值。如果能采用适当的裁剪方法，我们可以保留关键信息并丢弃离群值。这种裁剪将缩小量化的量化范围，从而减少量化误差。 根据这一观察，Min - Max量化不适用于激活的量化。为缩小量化范围，我们使用一个指标(L)来评估量化前后张量的距离，其公式为：

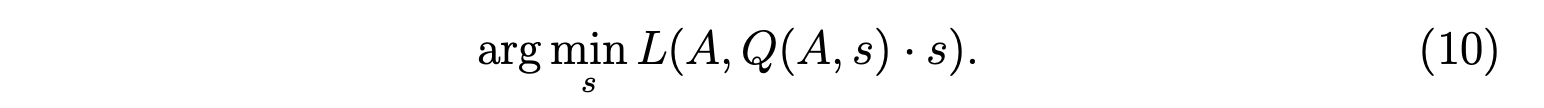
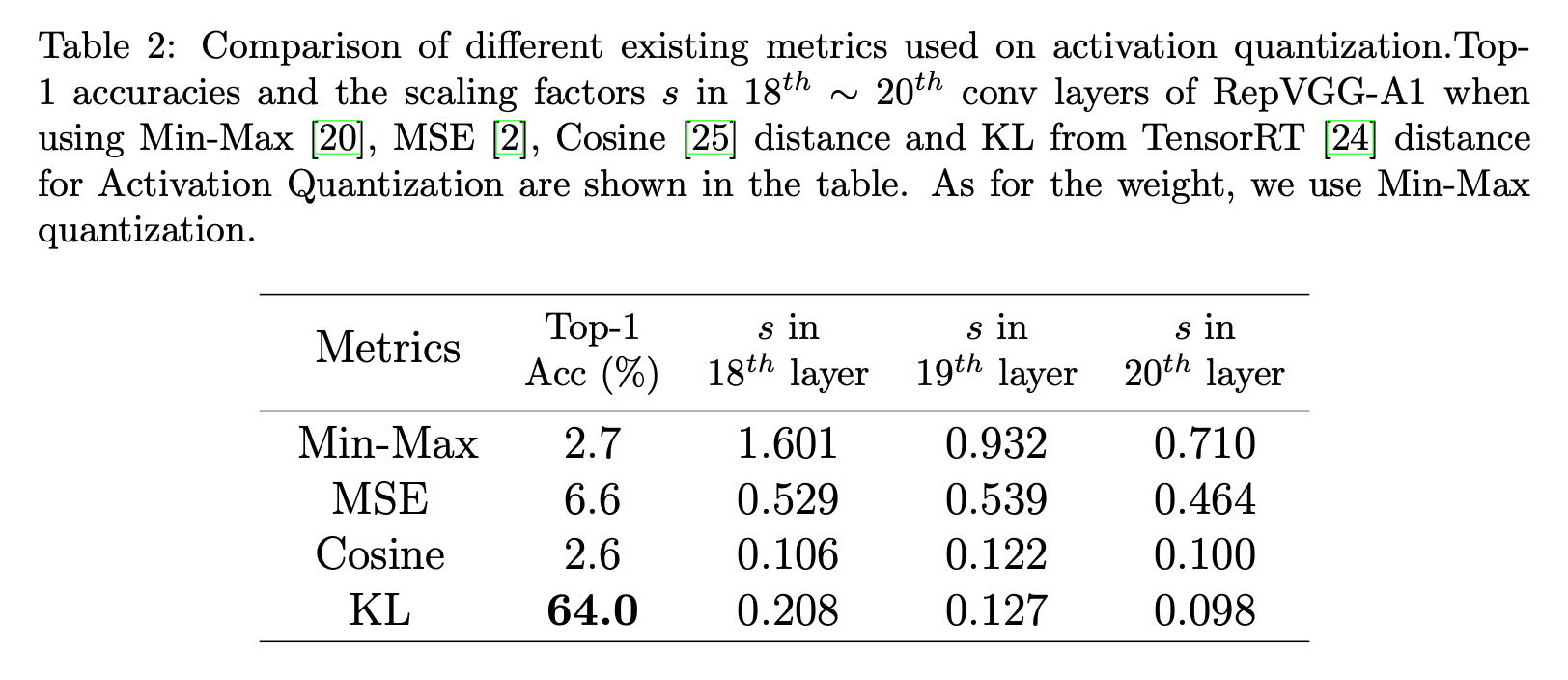
   有多种指标可用于评估两个张量的距离，如均方误差（MSE）、余弦距离和KL距离。之前基于重参数化网络的PTQ方法使用MSE作为激活量化的指标。然而，我们发现MSE指标并非最优。根据上述对激活分布的分析结果，存在许多对裁剪不敏感的较大值。但是，裁剪这些较大值会导致量化前后激活之间的MSE较大。因此，使用MSE指标的量化范围较大，并非最优。我们探索了不同的指标，并在表2中展示了结果。我们观察到KL指标优于其他指标。

   原始的KL指标在TensorRT中提出。然而，我们注意到在计算KL散度时存在一个数值问题，其公式为：

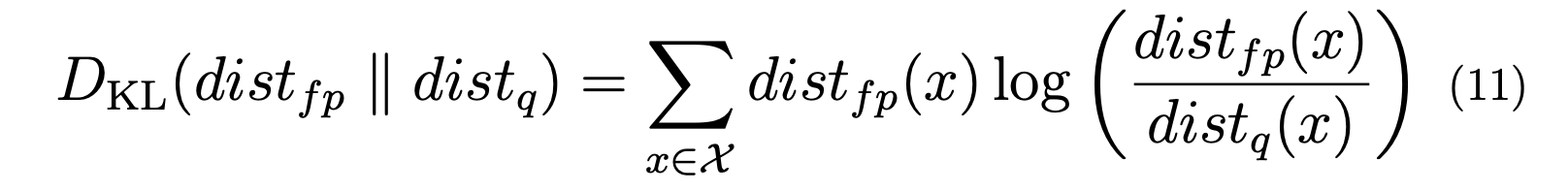
   其中(dist_{fp})是全精度激活的分布，(dist_q)是量化激活的分布，(X)是量化范围。由于分布值表示为浮点数，在计算 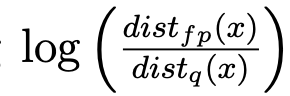时存在数值问题。有时结果会有显著误差，使得量化校准不准确。 为缓解此问题，我们建议变换计算方式：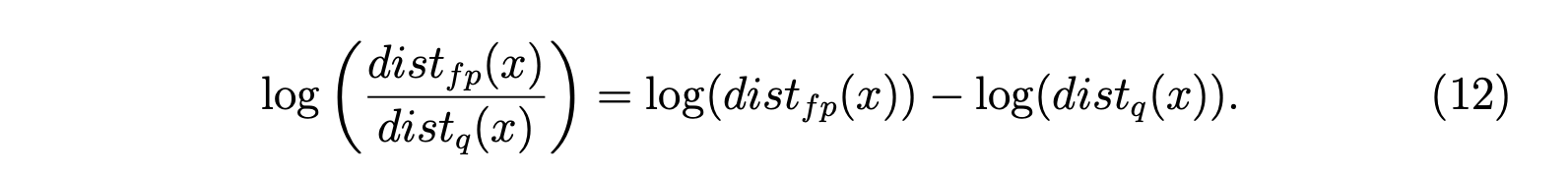

   

   如表3所示，变换后的计算实现了更好的量化结果。 在卷积层之后融合ReLU是常见的做法，这意味着卷积输出的激活值的负部分被裁剪。我们发现使用ReLU之后的分布来计算KL指标效果更好。表3展示了使用变换和ReLU融合进行基于KL量化的结果。

4. 实验评估

为了评估所提出的方法，我们在不同的基于重参数化的网络上进行实验。我们将介绍实验设置，然后分别展示在分类网络和目标检测网络上的实验结果。最后，我们将展示消融研究结果。

4.1 设置

我们在NVIDIA RTX3090上进行实验。在量化过程中的校准环节，仅使用32个未标记的校准样本。 我们针对不同规模的RepVGG网络[7]进行实验，包括RepVGG - A0、RepVGG - A1和RepVGG - B1，用于ImageNet [26]图像分类任务。RepVGG网络的输入是分辨率为224×224的RGB图像。我们还对基于重参数化的目标检测网络进行实验，包括YOLOv6t和YOLOv6s [11]。YOLOv6网络的输入是分辨率为640×640的RGB图像。我们使用32张未标记的校准图像对网络进行量化。 我们将所提出的方法与其他针对基于重参数化模型的量化方法进行比较，包括使用KL度量的普通训练后量化（vanilla PTQ）[24]、RepOpt [14]和QARepVGG [15]。这些方法的结果取自原始论文。

4.2 ImageNet图像分类

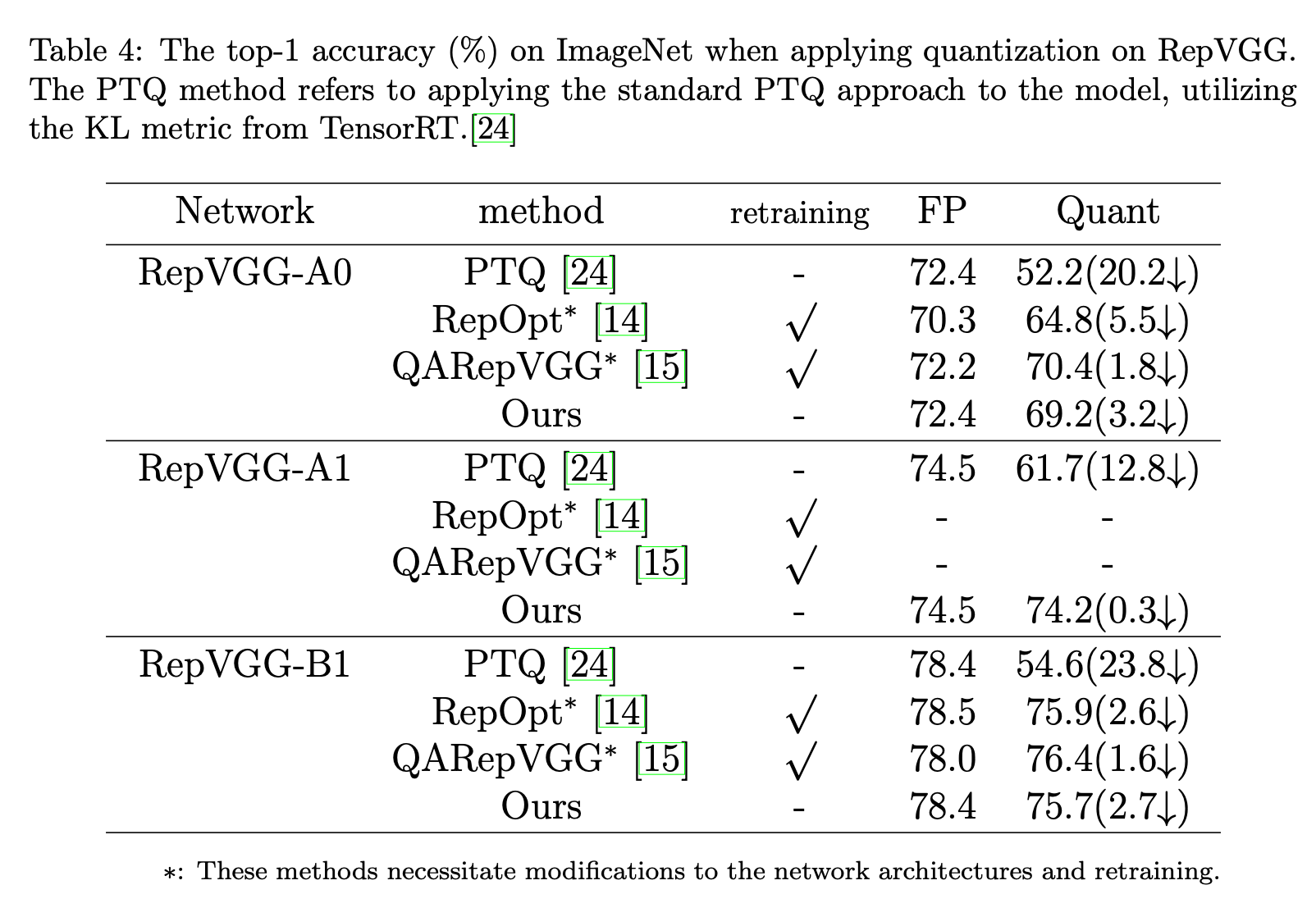
我们在表4中展示了全精度网络（FP）和量化网络（Quant）在ImageNet测试数据集上的Top - 1准确率。由于我们使用未经训练的原始RepVGG网络，全精度结果与原始结果相同。而RepOpt - VGG和QARepVGG对网络进行了重新训练，导致全精度结果较低。对于量化网络，普通训练后量化方法的结果大幅下降，这对于部署来说是不可接受的。得益于重新训练，RepOpt - VGG和QARepVGG在量化后取得了高得多的结果。量化后准确率的下降程度可用于公平比较。这种比较表明，我们的方法在量化网络上也取得了显著提升，与基于训练的量化方法相当。例如，我们在RepVGG - A0上实现了69.2%的Top - 1准确率，远优于普通训练后量化（52.2%），略优于RepOpt - VGG（64.8%），略逊于QARepVGG（70.4%）。

4.3 COCO目标检测

同样，在COCO目标检测测试数据集上，YOLOv6、其RepOptimizer方法及其QARepVGG方法的大多数平均精度均值（mAP）[27]取自[15]。此外，YOLOv6s及其RepOptimizer方法的性能由美团官方提供。表5中的实验表明，我们的方法在基于大规模目标检测的重参数化网络上具有泛化性。例如，我们在YOLOv6s上也实现了43.0%的mAP，下降了0.8%，远远超过普通训练后量化（41.2%），其下降了2.6%。我们还注意到，QARepVGG并非对所有网络都是最优的，下降了1.3%。

4.4 消融研究

我们对所提出的方法进行消融研究，结果如表6所示。我们观察到，结合ReLU融合的变换KL量化度量和粗 - 细权重拆分（CFWS）都能实现显著提升。例如，在RepVGG - B1上使用KL度量裁剪激活分布后，Top - 1准确率提升至62.0%。在对权重分布应用CFWS后，预测准确率提高到54.2%。然后，我们将这两种提出的方法结合使用，进一步提升了基于量化重参数化网络的性能（达到75.7%）。

1. 结论 本文提出了一种针对重参数化网络的新型训练后量化（PTQ）方法。我们提出粗 - 细权重拆分（CFWS）方法，以减少权重分布中的量化误差，并开发一种改进的KL度量，用于确定激活的最优量化尺度。我们的方法弥合了重参数化技术与实际PTQ部署之间的差距，在实现具有竞争力的量化准确率的同时，将准确率损失降至最低。CFWS方法有效地解决了重参数化网络量化过程中面临的挑战，使其在包括图像分类和目标检测在内的各种计算机视觉任务中更加高效且可扩展。