论文、代码和ppt地址：LSQ。代码地址: LSQplus

本文通过paper解读和代码的分析，来说明LSQ算法。

ABSTRACT

在推理阶段使用低精度运算的深度网络，相较于高精度的替代方案，具有功耗和空间方面的优势，但需要克服随着精度降低而保持高精度这一挑战。在此，我们提出了一种用于训练此类网络的方法——可学习步长量化（Learned Step Size Quantization），当使用多种架构的模型，并将权重和激活值量化到2位、3位或4位精度时，该方法在ImageNet数据集上实现了迄今为止最高的准确率，而且它能够训练出达到全精度基准准确率的3位模型。

我们的方法基于现有的量化网络权重学习方法，通过改进量化器本身的配置方式来实现。具体而言，我们引入了一种新颖的方法，用于估计并缩放每个权重及激活层量化器步长下的任务损失梯度，以便使其能够与其他网络参数一同被学习。这种方法可根据给定系统的需求使用不同的精度级别，并且只需对现有训练代码进行简单修改即可。

1 介绍

深度网络正逐渐成为众多革命性技术的组成部分，这些技术包括图像识别（克里日夫斯基等人，2012年）、语音识别（辛顿等人，2012年）以及驾驶辅助（徐等人，2017年）。要充分实现此类应用的潜力，需要从系统角度出发，将任务性能、吞吐量、能效以及紧凑性都作为关键考量因素，通过算法和部署硬件的协同设计来进行优化。当前的研究致力于开发创建深度网络的方法，这些方法在降低表示其激活值和权重所需精度的同时，能保持较高的准确率，进而减少其实现过程中所需的计算量和内存。使用此类算法为低精度硬件创建网络的优势已经在多个已部署的系统中得到了验证（埃塞等人，2016年；乔皮等人，2017年；邱等人，2016年）。

已有研究表明，低精度网络可以通过随机梯度下降法进行训练，在正向和反向传播过程中更新经过量化的高精度权重以及激活值（库尔巴里奥等人，2015年；埃塞等人，2016年）。这种量化是通过将实数映射到给定低精度表示所支持的离散值集合（通常是8位或更少位的整数）来定义的。我们希望针对每个量化层都能有一个能使任务性能最大化的映射，但如何最优地实现这一点仍是一个悬而未决的问题。

到目前为止，大多数训练低精度网络的方法都采用了均匀量化器，这种量化器可通过单个步长参数（量化区间的宽度）进行配置，不过也有人考虑过更复杂的非均匀映射（波利诺等人，2018年）。早期有关低精度深度网络的工作对量化器采用了简单的固定配置（胡巴拉等人，2016年；埃塞等人，2016年），而从拉斯特加里等人（2016年）的工作开始，后续工作侧重于根据数据来调整量化器，要么基于数据分布的统计信息（李和刘，2016年；周等人，2016年；蔡等人，2017年；麦金斯特里等人，2018年），要么试图在训练过程中最小化量化误差（崔等人，2018c；张等人，2018年）。最近，相关工作侧重于利用随机梯度下降法的反向传播来学习能使任务损失最小化的量化器（朱等人，2016年；米什拉和马尔，2017年；崔等人，2018b、2018a；荣格等人，2018年；巴斯金等人，2018年；波利诺等人，2018年）。

基于用户设置的固定映射方案虽然因其简单性而颇具吸引力，但并不能保证网络性能得到优化，而且量化误差最小化方案可能确实能将量化误差最小化，但如果采用不同的量化映射实际上能使任务误差最小化的话，那么它仍然不是最优方案。通过寻求最小化任务损失来学习量化映射的做法对我们很有吸引力，因为它直接致力于改进我们所关注的指标。然而，由于量化器本身是不连续的，这种方法需要对其梯度进行近似处理，而现有方法在进行这一操作时相对比较粗略，忽略了量化状态之间转换的影响（崔等人，2018b、2018a；荣格等人，2018年）。

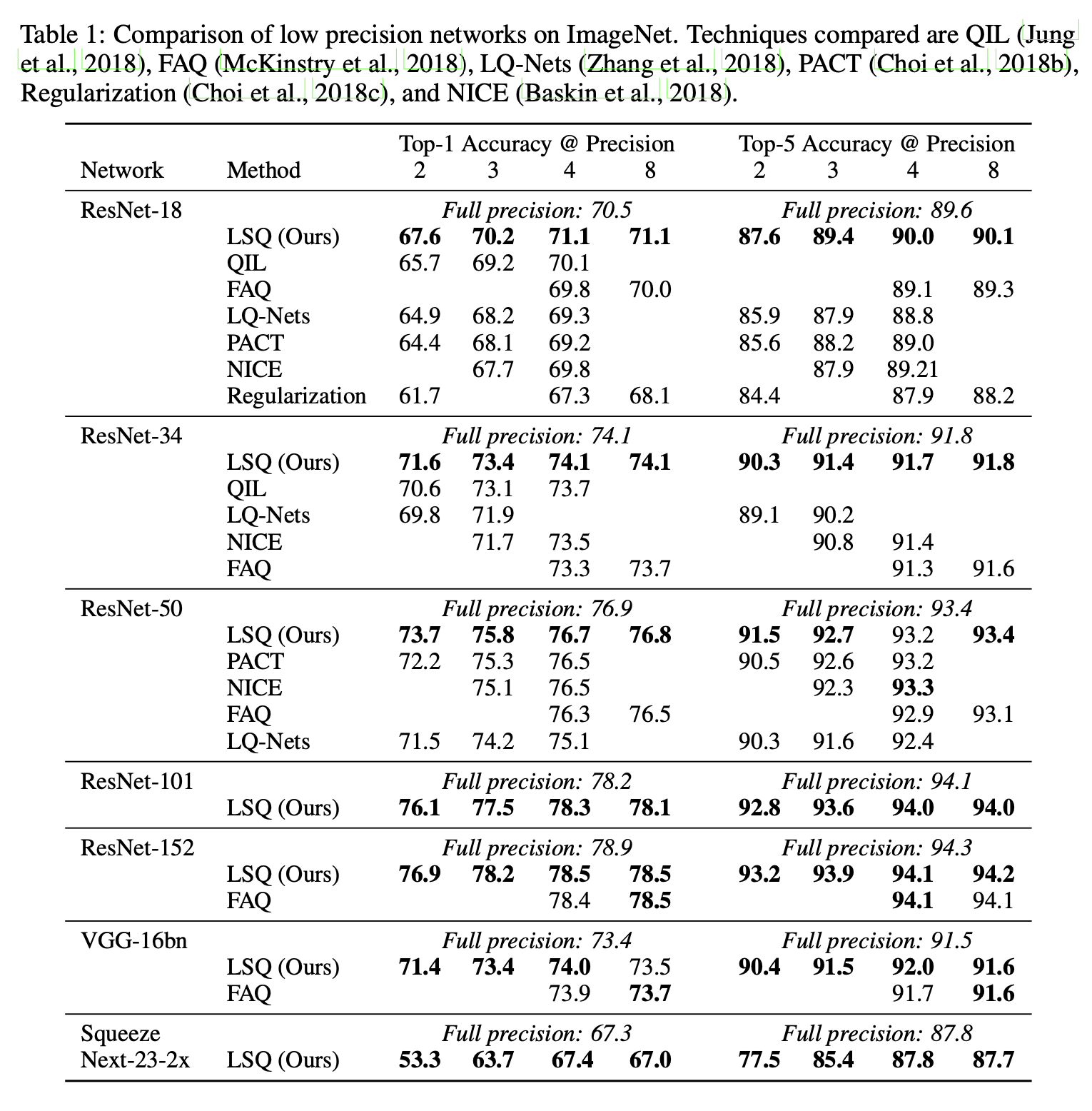
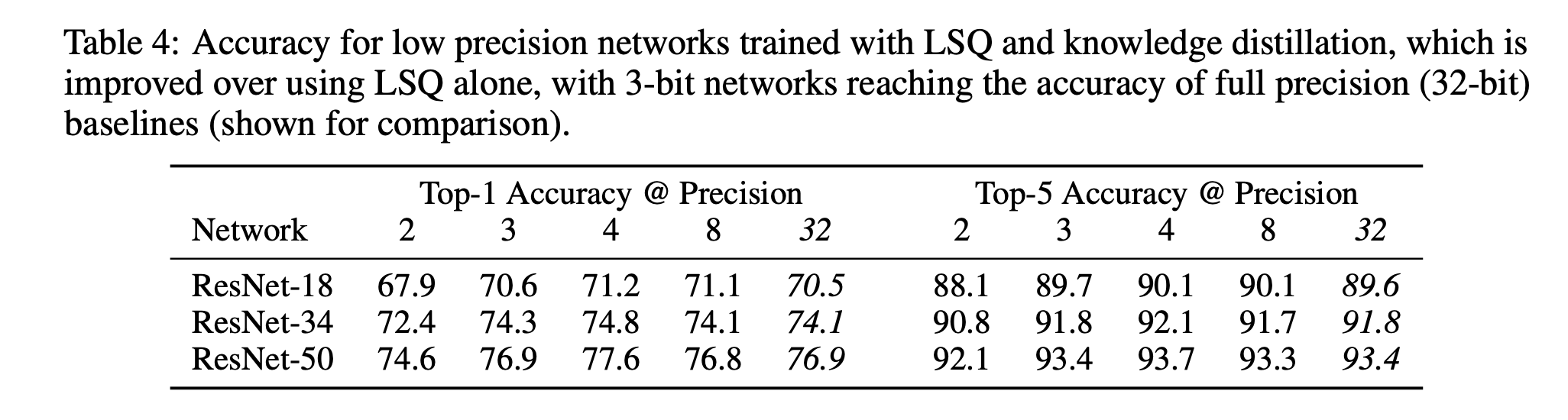
在此，我们介绍一种学习深度网络中每层量化映射的新方法——可学习步长量化（LSQ），该方法通过两项关键贡献对先前的研究成果进行了改进。首先，我们提供了一种简单的方法来近似量化器步长的梯度，该方法对量化状态转换较为敏感，可以说在将步长作为模型参数进行学习时，能够提供更精细的优化。其次，我们提出了一种简单的启发式方法，使步长更新的幅度与权重更新更好地达到平衡，我们证明了这有助于提高收敛性。整个方法可用于对激活值和权重进行量化，并且能与现有的反向传播和随机梯度下降方法配合使用。通过使用LSQ在ImageNet数据集上对多个网络架构进行训练，我们证明了其准确率明显优于先前的量化方法（表1），而且据我们所知，我们首次展示了3位量化网络达到全精度网络准确率这一里程碑式的成果（表4）。

2 实现方法

我们考虑在推理阶段使用低精度整数运算进行卷积层和全连接层计算的深度网络，这需要对这些层所使用的权重和激活值进行量化。给定要量化的数据v、量化器步长s、正负量化级别的数量QP和QN，我们定义一个量化器，它计算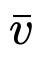（数据的量化且整数缩放表示）和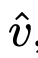（与v相同尺度的数据量化表示）：

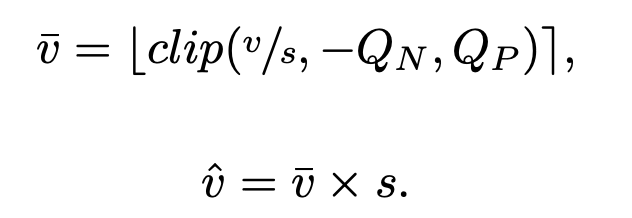
在此，clip(z, r1, r2)函数会返回这样的z：z中小于r1的值被设为r1，大于r2的值被设为r2，而⌊z⌉会将z舍入到最接近的整数。给定一个b位的编码，对于无符号数据（激活值），QN = 0且QP = 2^b - 1；对于有符号数据（权重），QN = 2^(b - 1)且QP = 2^(b - 1) - 1。

在进行推理时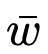，和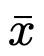值可作为低精度整数矩阵乘法单元（卷积层或全连接层的基础单元）的输入，然后使用成本相对较低的高精度标量 - 张量乘法将这些层的输出按步长重新缩放，这一步骤有可能通过代数运算与其他操作（如批量归一化）合并（图1）。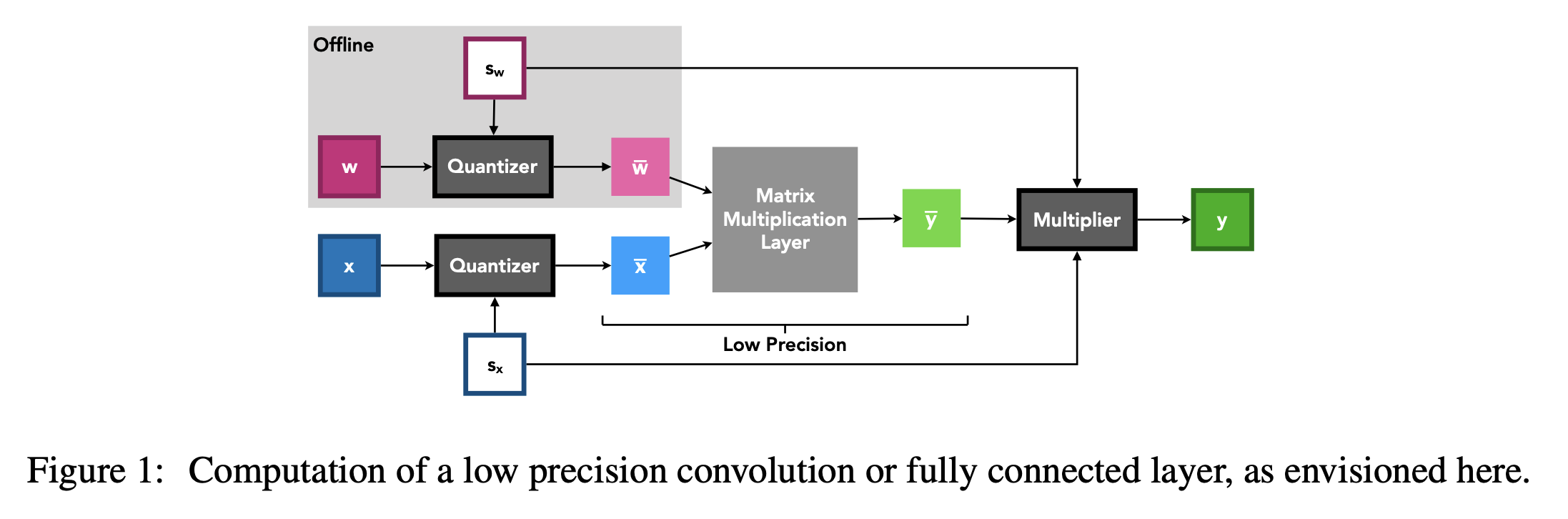

2.1 step size gradient

可学习步长量化（LSQ）通过向步长参数引入以下经过量化器的梯度，提供了一种基于训练损失来学习（量化器）步长s的方法。

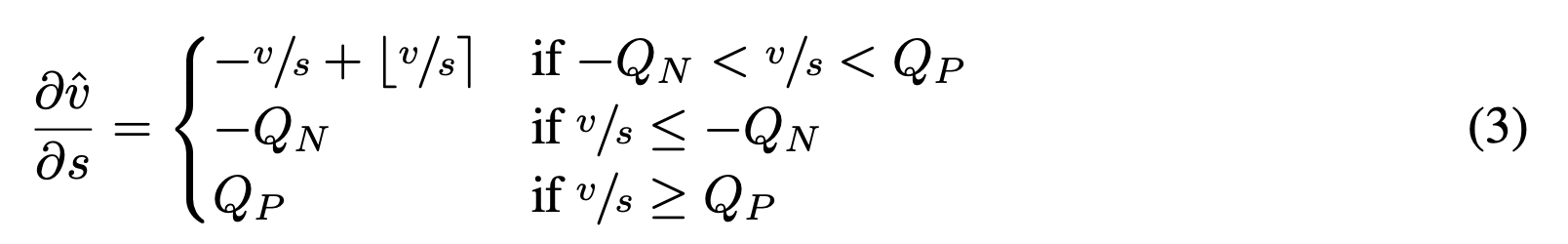
该梯度是通过直通估计器（本吉奥等人，2013年）推导得出的，它将取整函数中的梯度近似为直通操作（不过为了对下游操作进行求导，取整操作本身仍保留在原位），并对公式1和公式2中的所有其他操作正常求导。

该梯度与相关的近似方法有所不同（图2），那些相关方法要么学习一种完全在离散化之前就对数据进行的变换（荣格等人，2018年），要么通过从正向方程中去除取整操作、进行代数消项，然后求导使得当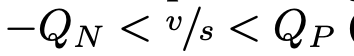时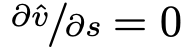（崔等人，2018b、2018a）来估计梯度。

在上述这两种先前的方法中，v与量化状态之间转换点的相对接近程度并不会影响到量化参数的梯度。然而，我们可以推断，给定的v越接近量化转换点，由于对s进行学习更新（因为此时s只需较小的变化），它就越有可能改变其量化区间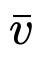，从而导致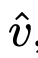出现较大的跳跃。因此，我们预期随着v到转换点的距离减小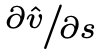，会增大，实际上我们在可学习步长量化（LSQ）梯度中也观察到了这种关系。令人欣喜的是，这个梯度很自然地从我们简单的量化器公式以及对取整函数使用直通估计器的操作中得出了。

在这项工作中，每一层权重以及每一层激活值都有一个不同的步长，以单精度浮点数（fp32）值表示，分别基于初始权重值或第一批激活值计算得出，并初始化为。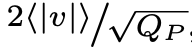

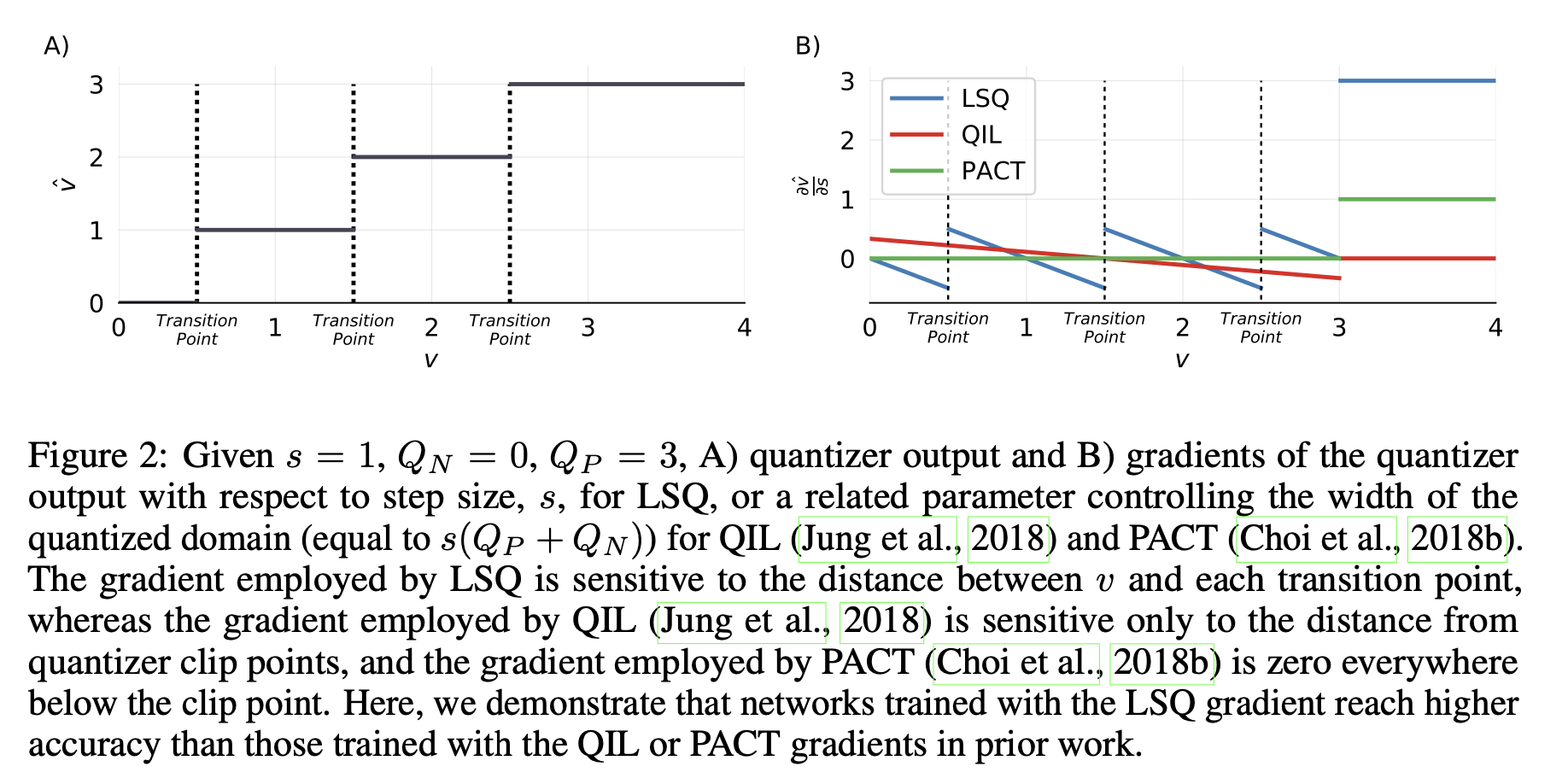图2：给定(s = 1)，(Q_N = 0)，(Q_P = 3)，A）量化器输出以及B）量化器输出相对于步长(s)的梯度（对于可学习步长量化（LSQ）而言），或者是相对于控制量化域宽度的相关参数（对于量化区间学习（QIL，荣格等人，2018年）和参数化裁剪激活量化（PACT，崔等人，2018b）来说，该相关参数等于(s(Q_P + Q_N))）的梯度。 可学习步长量化（LSQ）所采用的梯度对(v)与每个转换点之间的距离较为敏感，然而量化区间学习（QIL，荣格等人，2018年）所采用的梯度仅对与量化器裁剪点的距离敏感，而参数化裁剪激活量化（PACT，崔等人，2018b）所采用的梯度在裁剪点以下处处为零。在此，我们证明了使用可学习步长量化（LSQ）梯度训练的网络比先前工作中使用量化区间学习（QIL）或参数化裁剪激活量化（PACT）梯度训练的网络能达到更高的准确率。

2.2 step size gradient scale

已有研究表明，在训练过程中，当网络中所有权重层的平均更新幅度与平均参数幅度之比大致相同时，能够实现良好的收敛（尤等人，2017年）。一旦学习率得到恰当设置，这有助于确保所有更新既不会大到导致反复越过局部最小值，也不会小到导致不必要的漫长收敛时间。基于这一推理进一步拓展，我们认为每个步长的更新幅度与参数幅度之比也应当与权重的相应比例情况类似。因此，对于基于某个损失函数(L)进行训练的网络而言，该比率

平均而言，该比率应当接近1，其中∥z∥表示z的L2范数。然而，我们预计随着精度提高，步长参数会变小（因为数据被更精细地量化了），并且随着被量化项目数量的增加，步长更新量会变大（因为在计算其梯度时会对更多项目求和）。为了对此进行校正，我们将步长损失乘以一个梯度缩放因子g，对于权重步长，g = 1/√(NW×QP)，对于激活步长，g = 1/√(NF×QP)，其中NW是某一层中的权重数量，NF是某一层中的特征数量。在3.4节中，我们将证明这样做可以提高训练后的准确率，并且我们在附录A节中提供了选择这些特定缩放因子背后的理由。